Método de agrupamiento para el manejo de datos
El método de agrupamiento para el manejo de datos (en inglés: Group method of data handling, GMDH) es una familia de algoritmos inductivos para la modelación matemática computacional de conjunto de datos multi-paramétricos que caracteriza completamente la optimización estructural y paramétrica automática de modelos.
GMDH es utilizado en campos como Minería de datos, descubrimiento de conocimiento, predicción, modelado de sistemas complejos, optimización y reconocimiento de patrón.
Los algoritmos GMDH están caracterizados por el procedimiento inductivo que realiza un ordenamiento de modelos polinómicos gradualmente complicados y selecciona la solución mejor mediante el tan nombrado criterio externo.
Un modelo GMDH con múltiples entradas y una salida es un subconjunto de componentes de la función base (1):
donde f son las funciones elementales dependientes en diferentes conjuntos de entradas, a son coeficientes y m es el número de los componentes de la función base.
Para encontrar la solución mejor los algoritmos GMDH consideran varios subconjuntos de componente de la función base (1) llamados modelos parciales. Los coeficientes de estos modelos son estimados por el método de mínimos cuadrados. Los algoritmos GMDH gradualmente aumentan el número de componentes del modelo parcial y encuentran una estructura del modelo con complejidad óptima indicada por el valor mínimo de un criterio externo. Este proceso es llamado auto-organización de modelos.
La función base más popular utilizada en GMDH es el polinomio gradualmente complicado de Kolmogorov-Gabor (2):
Los modelos resultantes son también conocidos como redes neuronales polinómicas. Jürgen Schmidhuber cita a GDMH como uno de los métodos de aprendizaje profundo más tempranos, remarcando que ya en 1971 este fue usado para entrenar redes neuronales ocho-capas.[1]
Historia
[editar]El método fue desarrollado en 1968 por el Prof. Alekséi G. Ivájnenko en el Instituto de Cibernética de Kiev (en aquel entonces en la República Socialista Soviética de Ucrania).
Desde el principio, este enfoque inductivo era un método computacional, por lo que un conjunto de programas de ordenador y algoritmos fueron los resultados prácticos primarios obtenidos en la base de los principios teóricos nuevos. Gracias a la política del autor de código abierto, el método fue rápidamente establecido en el gran número de los laboratorios científicos mundiales. En aquel momento, compartir código era una acción completamente física, dado que el Internet es al menos 5 años más joven que GMDH. A pesar de este hecho, la primera investigación de GMDH fuera de la Unión Soviética fue realizada pronto por R. Shankar en 1972. Más tarde, científicos japoneses y polacos publicaron diferentes variantes de GMDH.
Periodo 1968-1971. Se caracteriza por la aplicación del criterio de regularidad única para la solución de los problemas de identificación, reconocimiento de patrones y predicción a corto-plazo . Como referencia fueron usadas funciones polinómicas, redes lógicas, conjuntos difusos de Zadeh y fórmulas de probabilidad de Bayes. La alta exactitud de predicción con la nueva aproximación fue un estímulo para los investigadores. No se investigó la inmunidad al ruido.
Periodo 1972-1975. Se solucionó el problema de la modelación de datos con ruido y base de información incompleta. Se propusieron la selección de criterios múltiples y la utilización de información adicional a priori para aumentar la inmunidad al ruido. Los mejores experimentos mostraron que con la definición extendida del modelo óptimo por un criterio adicional el nivel de ruido puede ser diez veces mayor que la señal. Posteriormente se mejoró mediante el teorema de Shannon de la teoría de Comunicación General.
Periodo 1976-1979. Se investigó la convergencia de los algoritmos GMDH multicapa. Esto mostró que algunos algoritmos multicapa tienen "multilayerness error" - análogo al error estático de los sistemas de control. En 1977 se propuso una solución de los problemas de análisis de sistemas objetivos por algoritmos GMDH multicapa. Esto dio como resultado que el ordenamiento por un conjunto de criterios encuentra el único sistema de ecuaciones óptimo y por tanto indica los elementos del objeto complejo y sus principales variables de entrada y de salida.
Periodo 1980-1988. Se obtuvieron muchos resultados teóricos importantes. Se mostró que no se pueden utilizar los modelos completamente físicos para predicciones a largo plazo. Se demostró que los modelos no físicos de GMDH son más precisos que los modelos físicos de análisis de regresión para la aproximación y la predicción. Se desarrollaron algoritmos de dos niveles que usan dos escalas de tiempo diferentes para modelar.
Desde 1989 se han desarrollado e investigado nuevos algoritmos (AC, OCC, PF) para la modelación no paramétrica de objetos difusos y SLP para los sistemas expertos. La etapa actual de desarrollo de GMDH puede describirse como el florecimiento de las redes neuronales dos veces-multicapa y los algoritmos combinatorios paralelos para ordenadores con multiprocesadores.
Criterio externo
[editar]El criterio externo es uno de las características claves de GMDH. El criterio describe los requisitos del modelo, por ejemplo minimización de mínimos cuadrados. Es siempre calculado con una parte separada de la muestra de los datos que no hayan sido utilizados para la estimación de los coeficientes. Hay varios criterios populares:
- Criterio de Regularidad (CR) - Mínimos cuadrados de un modelo en la muestra B.
- Criterio de Imparcialidad - Suma del valor del CR y el CR especial para el cual A es B y B es A. La proporción de la longitud de la muestra tiene que ser 1:1 i.e. el tamaño de A tiene que ser el mismo tamaño de B.
Si un criterio no define el número de observaciones para conjuntos de datos externos entonces aparece el problema de la proporción de división de los datos porque las capacidades de predicción del modelo identificado son muy dependientes de la proporción de división.
Redes neuronales tipo-GMDH
[editar]Hay muchas formas diferentes para escoger un orden para la consideración de los modelos parciales. El primer orden de consideración utilizado en GMDH y originalmente llamado procedimiento inductivo multicapa es el más popular. Este es un ordenamiento de los modelos gradualmente complicados generados por los polinomios de Kolmogorov-Gabor. El mejor modelo está indicado por el mínimo de la característica del criterio externo. El procedimiento multicapa es equivalente a la Red Neuronal Artificial con función de activación polinómica de neuronas. Por lo tanto, el algoritmo con tal aproximación es normalmente referido como Red Neuronal tipo-GMDH o Red Neuronal Polinómica.
GMDH Combinatorio
[editar]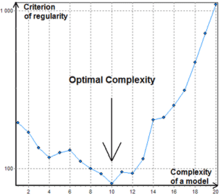
Otra importante aproximación en consideración a los modelos parciales cada vez más popular es una búsqueda combinatoria de fuerza bruta que puede ser tanto limitada o completa. Esta aproximación tiene algunas ventajas contra las Redes Neuronales Polinómicas pero requiere de un poder computacional considerable y por tanto no es eficaz para objetos con más de 30 entradas en caso de una búsqueda completa. Una consecuencia importante del GMDH Combinatorio es que este supera completamente la aproximación por regresión lineal si el nivel de ruido en el dato de entrada es mayor que cero.
El algoritmo combinatorio básico tiene los pasos siguientes:
- Dividir los datos de muestra en dos partes A y B.
- Generar estructuras para los modelos parciales.
- Estimar los coeficientes de los modelos parciales usando el método de mínimos cuadrados y la muestra A.
- Calcular el valor del criterio externo para los modelos parciales usando la muestra B.
- Escoger el mejor modelo (conjunto de modelos) indicado por el valor mínimo del criterio.
En contraste a las redes neuronales tipo-GMDH, el algoritmo Combinatorio no puede pararse en un nivel de complejidad seguro ya que in punto de incremento del valor del criterio puede ser simplemente un mínimo local, ver Fig.1.
Algoritmos
[editar]- Combinatorial (COMBI)
- Multilayered Iterative (MIA)
- GN
- Objective System Analysis (OSA)
- Harmonical
- Two-level (ARIMAD)
- Multiplicative-Additive (MAA)
- Objective Computer Clusterization (OCC);
- Pointing Finger (PF) clusterization algorithm;
- Analogues Complexing (AC)
- Harmonical Rediscretization
- Algorithm on the base of Multilayered Theory of Statistical Decisions (MTSD)
- Group of Adaptive Models Evolution (GAME)
Lista de softwares
[editar]- FAKE GAME Project — Código abierto. Multiplataforma.
- GEvom — Libre a petición para uso académico. Solo para Windows.
- GMDH Shell — Software de predicción para las empresas. Producto comercial con prueba libre. Solo para Windows. Algoritmos de aprendizaje: GMDH combinatorio y redes neuronales tipo-GMDH.
- KnowledgeMiner — Producto comercial. Mac OS X-único. Versión Demo gratis disponible.
- PNN Discovery client — producto Comercial.
- Sciengy RPF! — Software gratuito, Código abierto.
- wGMDH — Weka plugin, Código abierto.
- R Package para tareas de regresión – Software gratuito, Código abierto.
Enlaces externos
[editar]- www.gmdh.net — Artículos, libros y software.
- www.opengmdh.org — GMDH wiki y desarrollo de código
Referencias
[editar]Otras lecturas
[editar]- A.G. Ivakhnenko. Heuristic Self-Organization in Problems of Engineering Cybernetics. Automatica 6: pp. 207–219, 1970.
- A.G. Ivakhnenkofrf. Polynomial Theory of Complex System. IEEE Trans. on Systems, Man and Cybernetics, Vol. SMC-1, No. 4, Oct. 1971, pp. 364–378.
- S.J. Farlow. Self-Organizing Methods in Modelling: GMDH Type Algorithms. New-York, Bazel: Marcel Decker Inc., 1984, 350 p.
- H.R. Madala, A.G. Ivakhnenko. Inductive Learning Algorithms for Complex Systems Modeling. CRC Press, Boca Raton, 1994.


